Risk analysis with a genetic algorithm and TrueSkill

While (data) science is in principle about finding a solution to a
problem, sometimes I find myself looking for a problem that suits
a certain solution. This post results from such a situation: I was
looking for an interesting problem to apply a genetic algorithm to.
I had never used any evolutionary algorithm and wanted to play around
with one. When Vincent decided to scrutinize monopoly
I realized that (board) games make excellent subjects to try out some
algorithms. So here we are… genetic algorithms for Risk!

The game of Risk

As you may well know, Risk is a strategic board game for 2 to 6 players
that revolves
around conquering (a tabletop version of) the world. It was invented
in 1957, and has been quite popular ever since. Detailed rules of the
game can be found here,
but I’ll a very short introduction to the game to get you started.

The game revolves around the game board, which is shown below. The board
resembles a map of the world, divided into 42 territories spread over
six continents, each with a different color.
Territories are considered adjacent if their borders
touch or if they are connected by a dotted line.

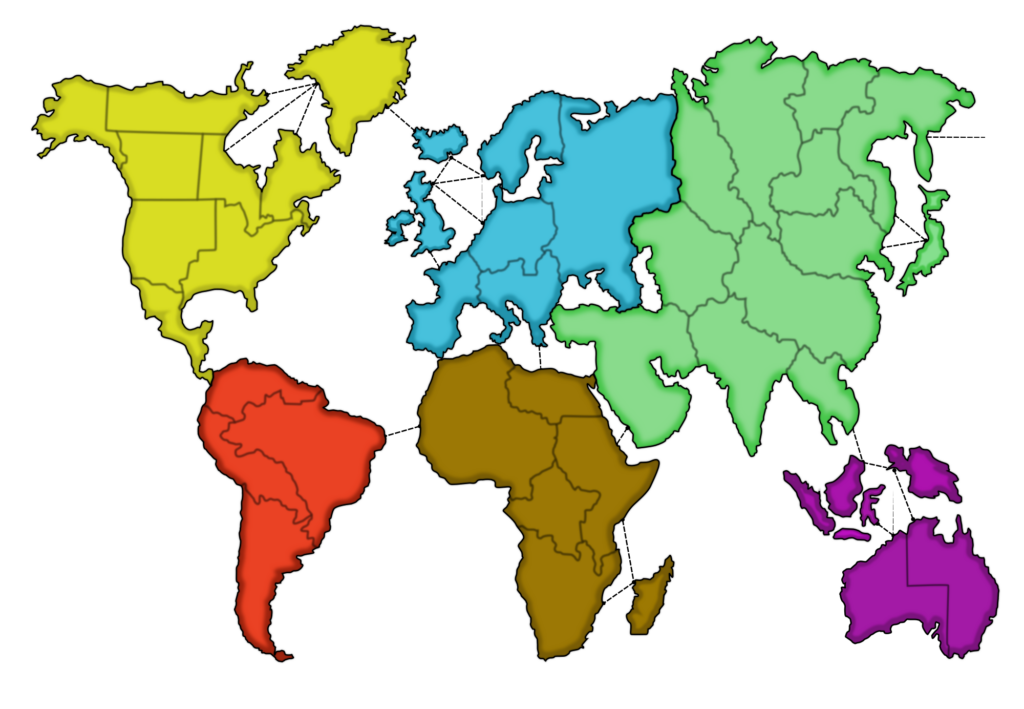
At the start of the game the territories are randomly distributed
amongst the players. Each player gets a number of armies to place on
his territories. Also, each player is given a mission which he needs
to complete to win the game. Missions range from conquering specific
continents, a number of territories or eliminating another player.

Then players get to play their turns one by one until a player achieves
his mission. A turn consists of three stages:

Reinforcement, during which the player places additional armies.
The number of armies depends on the territories in his control.
Combat, during which the player may attempt to conquer other
territories.
Fortification, during which the player may move armies.

The odds in combat are decided using dice, where the defending party
has better odds unless the attacker has many more armies.

In general, a good strategy is to conquer full continents, as a player
that controls one or more full continents at the start of his turn
receives extra reinforcements. But of course the game is not so simple
and one can have many strategies.

A genetic Risk player

The principle of a genetic algorithm (GA) is based on natural selection
and evolution: given a number of solutions, one selects a number of
the best solutions and the modifies (mutates) and combines these to
form a new generation of solutions.

An implementation of a GA requires a genetic representation of a
solution as well as a fitness function to evaluate the quality of the
solutions. Neither of these requirements is trivial in the case of
Risk.

Genetic representation

Our solutions, the Risk players, need to be designed such that we can
perform the basic genetic operations on them: we need to be able to
mutate and
combine
them. The easiest way to allow this is to find a vector representation
of the player. A mutation is then simply a change in one or more of the
elements (genes) of the vector (genome), and combining can be done by
taking one genome and replacing some of the genes by those of another
genome.

A simple python implementation of such a genome could look like this:

class Genome(object):

    def __init__(self, genes):
        self.genes = genes

    def combine(self, other):
        return Genome([
            mine if random.choice([True, False]) else theirs
            for mine, theirs in zip(self.genes, other.genes)
        ])

    def mutate(self):
        return Genome([random.gauss() + val for val in self.genes])

The player needs to make decisions based on the genome, of course.
For example, it needs to decide where to place armies in the
reinforcement phase. We can
achieve this by computing some score (‘rank’) for every territory it can
place an army on, and then placing the army on the territory with the
highest rank. This rank can depend on many features of the territory,
such
as the number of armies on it, the number of hostile armies around it
and the value of the territory to the players’ mission. We can use the
genes, the elements in the genome, as weights to the various features
that make up the rank.

So, for each army a player may place in the reinforcement phase, we
calculate a reinforcement rank $R_r$ for each territory it can place
the army on. This rank is based on various features of the territories,
weighted using the genes of the player:

 $R_r = \sum_i (f_i * w_i),$

where $f_i$ is a feature of the territory, and $w_i$ is the weight the
player assigns to that feature. Then the army is placed on the territory
with the highest rank.

Features of a territory can be, for example:

army vantage: the ratio of hostile armies on neighboring territories
to the number of armies on the territory in question,
territory vantage: the ratio of neighboring territories that are
hostile,
mission value: whether or not the territory is valuable to the
mission of the player. This depends on the mission, of course.

We can implement a player object based on the above implementation of
the Genome class:

class Player(Genome):

    def place_reinforcement(self, board):
        return max(board.my_territories(), key=lambda t: self.reinforcement_rank(t))

    def reinforcement_rank(self, territory):
        return army_vantage(territory) * self.genes[0] + \
            territory_vantage(territory) * self.genes[1] +\
            mission_value(territory) * self.genes[2]

Similarly we can construct an attack rank and a fortification rank.
Many of the features are shared between the ranks: if for example the
mission is important for determining where to place armies it is
likely also important for deciding which territory to attack. The
weights however should not be shared as the motivations for the actions
in each phase are different: when attacking one tries to obtain new
territories or exterminate a player, while during fortification one may
want to fortify his most valuable territory.

In the attack phase we need not only decide which territory to attack,
but also whether to attack at all. This can be done by calculating the
attack ranks for all attack options, and only attacking if the highest
attack rank is above a certain threshold. The ideal level of this
‘attack threshold’ can also be determined by the GA by making it one of
the genes.

Finally we need to think about the domain of the weights: if all of the
weights $w_i$ are left unrestricted we run the chance that they run off
to infinity. It is not so much the value of each weight but the ratio
between them that influences the final decision. Hence we need to set
an absolute scale. We can do that by restricting one of the weights
to the values $-1$ , and $1$ . As long as this weight does not
converge to this will set a scale for the other weights.

Fitness function

Now we have a genetic representation of a player, we need to be able
to evaluate it. Of course the ‘quality’ of a single player
cannot be evaluated; and is probably even impossible to define. On the
other hand, it is not so difficult to find out whether one player is
better than another: we could simply let them play a game and see who
comes out as a winner. As Risk is not really suited for two players we
can have multiple (for example four) players compete in one game, which
has the advantage that we can evaluate multiple players in a single
game. Of course there is a factor of chance, but we can have the
players play several games to properly evaluate which is (are) the
better player(s).

Now this works well if we have only a few (up to six) players. When we
are going to evaluate more players, having each player compete
with each other player quickly goes out of hand. For a hundred players
that would require many hundreds of millions of games.

Luckily, the problem of ranking players of a game has been solved
before. Microsoft developed a ranking system called
TrueSkill to rank players
on Xbox Live. While the exact implementation used by Microsoft has not
been made public, a python implementation that mimics its behaviour
is publicly available. An interactive
explanation of the workings of TrueSkill can be found
here.

So using TrueSkill, we can have the players play multiple games in
randomly selected groups until we are satisfied with the $\sigma$ s of
the TrueSkill beliefs and then select players based on their $\mu$ s.

Results

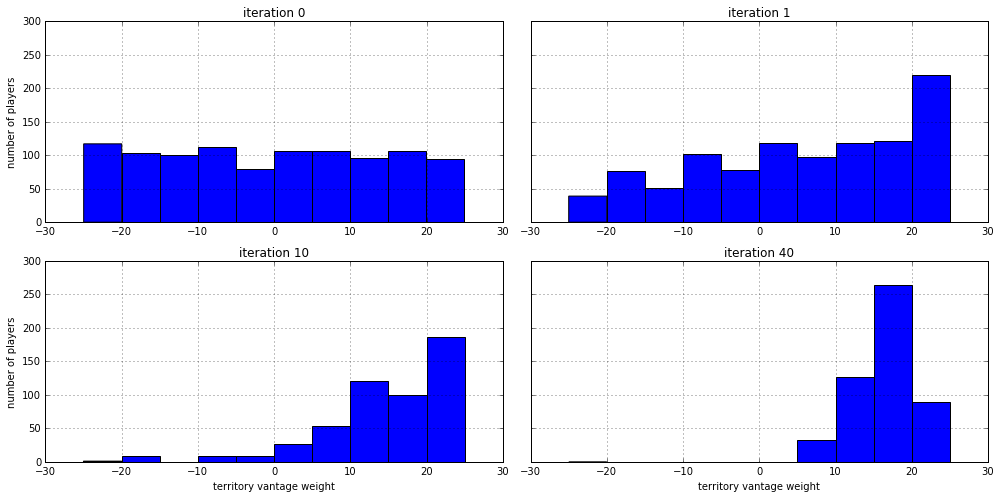
So, does this approach actually work? Yes, it does! See below the
distributions of weights ( $w$ ) for the territory vantage feature
described above. Initially it was evenly distributed over the range
$[-25, 25]$ , but after a single iteration of the GA we already see
it favors the positive side, meaning that it is better to place armies
on territories that have a lot of hostile neighbors. After ten
iterations there are hardly any players left that have a negative weight
for the territory vantage feature, and after forty iterations we see
it peaking around a weight just below twenty.

Now I could take you through all other features, but I think that would
get boring pretty soon. If you want to play around with the genetic
player or Risk in general, you can find the implementation I used
here. If you do want
some more information before having a look at the code,
see the talk
I gave at Europython.

Mind you, it doesn’t always go as smoothly as the above figure would
let you believe. For example, in the initial (random) population there
are some players which have the above-mentioned ‘attack-threshold’
at such a high level that they would never attack. If you happened to
have a game with only such players, no attack would ever happen and the
game would go on indefinitely.

Of course the ‘best’ player that came out of the algorithm is by no
means the best player that could exist. First of all, the algorithm
hadn’t really converged after 40 iterations (about 12 hours in), so
running a little longer could yield (much) better results. Also, most
likely some features exist that are much better than those
I constructed. And in the end this algorithm is limited in any case
since it only makes
linear combinations of some constructed properties and it does not
have an internal state to keep track of other players’ behavior.

Nonetheless it is a fun way to experiment with genetic algorithms!

Mike Izbicki used the Risk Analysis in his lectures at Claremont McKenna College.
"GoDataDriven has helped me develop cutting edge data analysis courses for
the students at Claremont McKenna College," Izbicki shared with us,